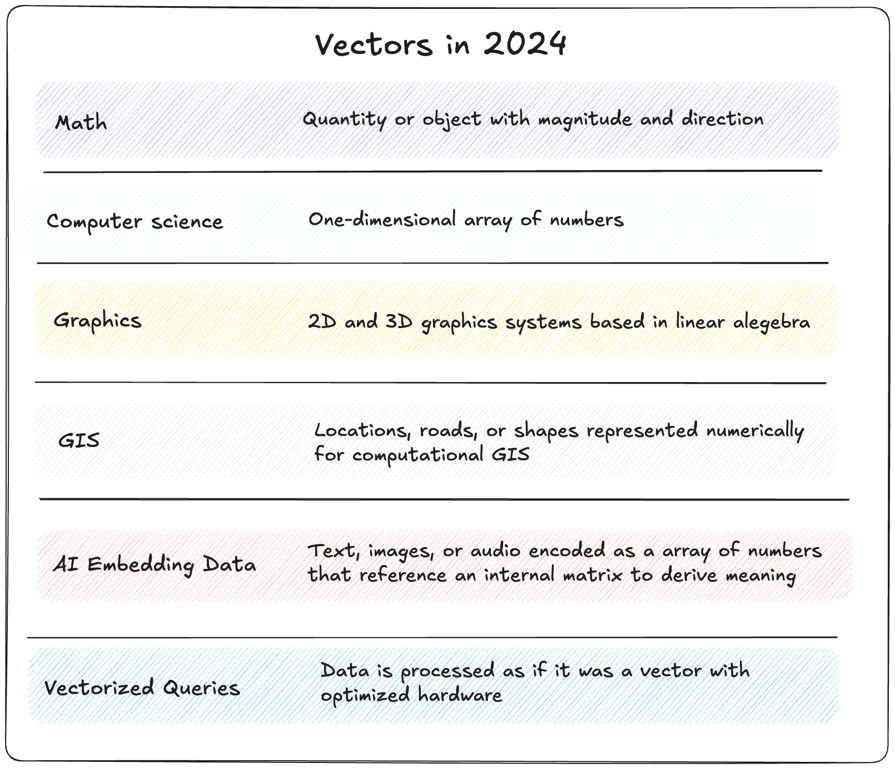
I can’t get through a zoom call, a conference talk, or an afternoon scroll through LinkedIn without hearing about vectors. Do you feel like the term vector is everywhere this year? It is. Vector actually means several different things and it's confusing. Vector means AI data, GIS locations, digital graphics, and a type of query optimization, and more. The terms and uses are related, sure. They all stem from the same original concept. However their practical applications are quite different. So “Vector” is my choice for this year’s name collision of the year.
In this post I want to break down the vector. The history of the vector, how vectors were used in the past and how they evolved to what they are today (with examples!).
The idea that vectors are based on goes back to the 1500s when René Descartes first developed the Cartesian coordinate XY system to represent points in space. Descartes didn't use the word vector but he did develop a numerical representation of a location and direction. Numerical locations is the foundational concept of the vector - used for measuring spatial relationships.
The first use of the term vector was in the 1840s by an Irish mathematician named William Rowan Hamilton. Hamilton defined a vector as a quantity with both magnitude and direction in three-dimensional space. He used it to describe geometric directions and distances, like arrows in 3D space. Hamilton combined his vectors with several other math terms to solve problems with rotation and three dimensional units.

The word Hamilton chose, vector, comes from the Latin word vehere meaning ‘to carry’ or ‘conveyor’ (yes, same origin for the word vehicle). We assume Hamilton chose this Latin word origin to emphasize the idea of a vector carrying a point from one location to another.
There’s a book about the history of vectors published just this year, and a nice summary here. I’ve already let Santa know this is on my list this year.
Building upon Hamilton’s work, vectors have been used extensively in linear algebra pre and post computational math. If it has been 20 since you took a math class here’s a quick refresher.
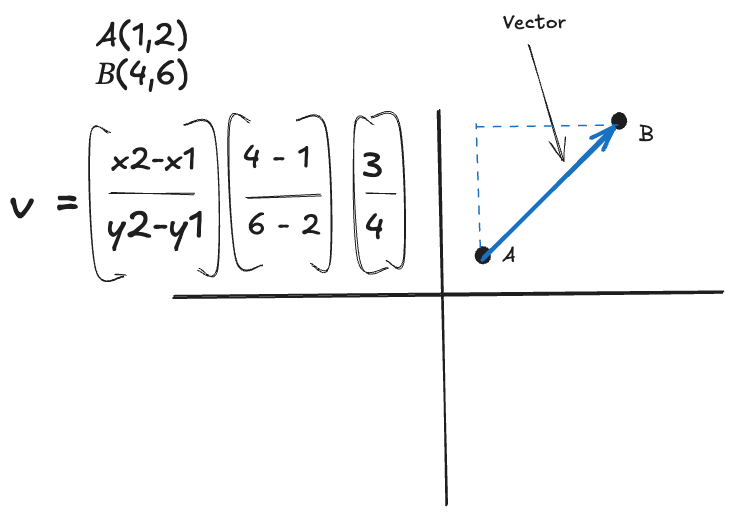
Linear algebra is a branch of mathematics that focuses on vectors, matrices, and arrays of numbers. Here’s a super simple mathematical vector equation. We have two points on an XY coordinate system, point A at 1, 2 and B at 4,6. The vector formula for this is below in this diagram, final solution 3,4.
Linear algebra of much more complicated forms is used in solving systems of linear differential equations. Vector equations have practical use cases in physics and engineering for things we use every day like heat conduction, fluids, and electrical circuits.
Early computer scientists made heavy use of the vector in a variety of ways. A computational vector can be similar to the example above or even just a simple numeric array of fixed size with where the numbers have related values. In early computer programming, simple operations like additions or subtraction would be applied to a set of vectors.
A basic example of this could be financial portfolio analysis where you have two vectors: 1 - Portfolio weights, v1, showing the proportion of investment in different stocks and 2 - market impact adjustments, v2, that adjusts markets based on current values. This code sample here in C calculates the adjusted weights for each stock in the portfolio by adding the two vectors.
#include <stdio.h>
#define STOCKS 8
typedef float Portfolio[STOCKS];
int main() {
// Portfolio weights (in percentages, out of 100)
Portfolio portfolioWeights = {10.0, 20.0, 15.0, 25.0, 5.0, 10.0, 10.0, 5.0};
// Market impact adjustments (positive or negative percentages)
Portfolio marketAdjustments = {0.5, -0.3, 1.0, -0.5, 0.2, -0.1, 0.0, 0.7};
Portfolio adjustedWeights;
// Perform vector addition
for (int i = 0; i < STOCKS; i++) {
adjustedWeights[i] = portfolioWeights[i] + marketAdjustments[i];
}
// Print adjusted weights
printf("Adjusted Portfolio Weights: <");
for (int i = 0; i < STOCKS; i++) {
printf("%s%.1f%%", i > 0 ? ", " : "", adjustedWeights[i]);
}
printf(">\n");
return 0;
}
Modern computer science builds on similar concepts of organizing and processing collections. The std::vector in C++ and Vec<T> in Rust are general-purpose dynamic arrays. They can be virtually any data type to help manage or compute collections of elements.
Vector graphics were used in early arcade and video game development. Think of something like Spacewar! or Asteroids. Vectors could be used to draw lines and shapes like ships and stars.
Here’s a super simple example of how vectors could be used to draw a triangle.
#define DrawLine(pt1, pt2)
typedef struct Point {
int x, y;
} Point;
typedef struct Line {
Point start;
Point end;
} Line;
Line lines[3] = {
{{0, 0}, {100, 100}}, // Line 1
{{100, 100}, {200, 50}}, // Line 2
{{200, 50}, {0, 0}} // Line 3
};
// Loop through these points to draw our triangle on the screen.
int main()
{
for (int i = 0; i < 3; i++)
{
DrawLine(lines[i].start, lines[i].end);
}
return 0;
}
These early xy arrays and computerized graphics paved the way for modern computer graphics which make use of vectors in even more advanced ways. When you play a modern 3D video game, many characters, objects, and movement you see on the screen are powered by linear algebra vectors.
The Graphics Processing Unit (GPU) was a specialized computer developed in the 1990s and then improved on in the decades since. GPUs handle the millions of vector operations required to create 3D graphics in real time. GPUs now are used for far more than 3D graphics. Vector-based assembly operations can operate on a continuous block of memory, doing the same operation across different chunks of memory.
Scalable vector graphics (SVG)
SVGs are 2D vector graphics that have become a de-facto image format in web design and development. There’s a vector standard that allows svg graphics to be created with a series of numbers that represent shapes and paths that work across devices and web browsers. SVG graphics display logos, icons, charts, and animations. Their popularity took off in the mid 2010s and continues to grow as they remain popular due to their performance and lightweight nature.
SVGs use some number of vector numbers to describe the object they represent. For a simple SVG with a few shapes might be dozens of numbers. A more complex SVG like one for a detailed icon or map might include thousands of numbers.
Here’s what the SVG of the Crunchy Data hippo logo looks like:
<svg
id="aad9811e-aeeb-4dae-a064-7d889077489a"
data-name="Layer 6"
xmlns="http://www.w3.org/2000/svg"
viewBox="0 0 1407.15 1158.38"
>
<path
d="M553.21,651l124.3,122.4-154.9-89Zm-304.5-496.6-54.6,148.9L35.71,415.19,6.81,523.49l-6.5,67.9,83.1,65.2h0l208.7-10.3,114.1-155.7,3.6-166,199.3-200.5-104.7-41.9Zm0,0,360.4-30.3m-104.7-41.9-114.1,61.4-130.7,213.5-105.5,150.5-70.8,149m322.9-166-145.9-135.4-222.5,62.1M294.21,642l-140.1-135.1L1,586.39m36.1-171.2,116.3,91,190.8-73.1m-95.5-278.7L259.61,357m150.1-32.4-19.4-181m218.8-19.5,14.7,196.7-59.5,137.4-49.1,104-92.7,47.2-128.8,35.9,139.8,39.3L621.21,632l62.4-196.3,16.7-174.4-92.4-136.9M621.21,632l-215-141.5,26.7,194-349.6-28m617-395.2-294.1,229.3,215,141.5m-217.1,50.2,8.6,306.7-17.5,35.7,6.1,52.8,101.7-4.8,63.5-63.9,6-47.9L588.41,792h0l89.2-18.4,97.2,23.4,84.2,19.7-2.1,46.5,10.5,30.4-19,28.9,28.1,1.9,1.6-.8,6,105.5-15.1,40.1,25.3,88.7,132.1-33-6.1-50.6,65.5-306.8,49.5-12.2,57-43,29,41.1,2.4,88.3,5.8,61.8-18.6,46.2,23.5,38.7,96.5-12.4,44.3-43.5-21.1-28.8,13.8-216.9,4-65.5,34.6-116.4-23.4-120.4-332.8-215.1L842,135l-151.2,47.5m119.9,84.8-202.4-143.1m202.4,143.1L849,552.39l134.2-214.2ZM1164,453.09l-180.8-115-42.6,277Zm-486.5,320.4,263-158.4L849,552.39Zm133.2-506.2-110.6-4-4.6,48.5,115-42.3m-133,504-154.9-89,65.7,107.4Zm170.3-25.9,35.1,87,57.6-219.4Zm117.7,83.3-25-215.8-57.6,219.4Zm-24.9-215.8,25,215.8,120.2-63.5Zm12.7,418.8,94-83.9-81.9-119.1Zm-105.5-285.6-170.3,25.2,200,47.7ZM1164,453.09l-70.6,270.3,141.1-114Zm70.5,156.3,77.8-132.8L1195,262.89Zm-251.3-271.3,180.8,115,31.1-190.2Zm67.1-168.8-67.1,168.8,211.9-75.2ZM842,135l-151.2,47.5,359.5-13.9Zm244.2,633.2,7.2-44.8m167.2-63.1,51.8-183.7-77.9,132.8Zm0,0-26.1-50.9-99.3,145.8Zm0,0,84.1-88.7-32.4-95Zm84.1-88.7-84.1,88.7,42.4-7.6Zm-22.6-226.7-9.8,131.7,32.4,95Zm0,0,22.6,226.7,62-69Zm46.3,339.3-65.3-30.2,56.7,161.5Zm-114.7,122.3,77.3-31.9-28.1-121.8Zm49.2-153.7,28.1,121.8,28.9,40.9Zm69.3-32.3-27.5-48.9,23.7,112.6ZM1331,774.59l-4.7,123.7,33.6-82.7Zm-93.9,213.3,94.5-12.7-5.4-78.4Zm16.6-181.4-30,35.1,13.4,139.9,63.4-138.2Zm0,0-33.1-115.9,3.1,150.6Zm-32.8-115.2,82.2-37.2m-73.5,249.3,7.6,84.6m94.5-12.8,43.7-42.9-49.1-35.5Zm-5.8-79.2,29.1,7.3m-942.3,85.6-11.4,88.5,63.4-55.8Zm51.2,31.9,38.7,52.5,63.8-64.5Zm556,53.9-66.6-40.8-59.2,123.9Zm-431.6-282.8-112.2,70.4-11.4,159.3Zm-178.6,89.3,2.9,107.7,63.5-126.6Zm238-729.1,40.7-57.4L702,45.29l-13.6-32L650.11.49l-13.6,2.6-31.2,41.3-10.3,73,14.1,6.7ZM650,.49l-48.6,74.7,81.4-45.9Zm32.7,28.4L702,45.19m-19.1-15.3,5.5,64.8L647.31,110l-38.2,14.1m0,0-7.7-48.9m87-61.9-5.5,16.6L650,.59m-269.3,116-4.1-59.1-45-22.9-43.7,26.8,2.7,42.8,11.5,35.3M346.21,81l-14.6-46.5-41,69.7L346.21,81l-43.8,58.5m74.2-82.1L346.21,81l34.5,35.6m486.4,777.9,10.9,29m4.9-90.7-15.6,60.6,10.7,30.1Zm-407,32,46.7-180.3-112.9,196.7m23.2-196.6,89.7-.1,30.6-33.4M744.81,394l-10.6,113.9L849,552.39Zm-75.5,84.8L621.21,632l113.1-124.1Zm64.9,29.1-56.7,265.6m0,0,27.2-133.3-83.6-8.1Zm68.1-380.1-59.2,18m9-99.7,49.4,82.3,65.7-124.6Zm-289.2,178.9,277.3-54.9m200.3,594.7,31-31.4,50.7-168.1m-82.6,1.9,31.9,166.1,38.5,34.9M1331,774.59l-30.4,68.7,25.8,53.5M287.91,61.39l23.9,6.7"
fill="none"
stroke="currentColor"
stroke-linejoin="bevel"
/>
</svg>
In modern computational GIS, vectors are used to represent geometric data types like points, line-strings, and polygons. Like any other x,y,z vector coordinate system the vectors refer to specific global points or objects. There’s quite a few different spatial reference systems that can be used. The vectors are typically stored in PostGIS using a binary format Well-Known Binary (WKB), which is a standardized binary encoding for geometries. Vectorization also powers many of the key functions in modern geospatial data processing like intersections, distance calculations, joins, and proximity analysis.
Here’s the vector binary for (imho) the best BBQ restaurant in the world:
restaurant_name | geom
-----------------+----------------------------------------------------
Gates Bar B Q | 0101000020E610000082E673EE76A557C007B47405DB884340
AI vectors emerged from the mathematical and computational foundations of vectors that I covered above. Through advancements in hardware and in machine learning algorithms, vectors can be used as a system to describe virtually anything. Large Language Models (LLMs) convert data like text, images, or other inputs into vectors through a process called embedding. LLMs use layers of neural networks to process the embeddings in a specific context. So the vectors numerically represent relationships between objects within the context they were created with.
You’ve probably heard of the pgvector extension that is used for storing and querying AI related embedding data. pgvector adds a custom data type vector for storing fixed-length arrays of floating-point numbers. pgvector stores up to 16k dimensions.
My colleague Karen Jex has a great embedding talk she does about AI called “What’s the Opposite of a Corn Dog”. The vector embedding for a corn dog from an OpenAI menu dataset is an array of a staggering 1536 numbers. Here’s a snippet.
// vector of a Corn Dog
[0.0045576594,-0.00088141876,-0.014024569,-0.011641564,0.0038251784,0.010306821,-0.01265076,-0.013672978,-0.01582159,-0.041670028,0.0044274405,.........0.040185533,-0.010463083,0.004326521,-0.019571891,0.01853014,0.025770308,-0.017787892,0.0018572462]
In AI and machine learning, a vector is an ordered list of numbers that represents data for literally anything. Really what “AI” is doing is turning anything and everything into a vector and then comparing that vector with other vectors in the same matrix.
As the use of computational vectors have become so popular along with machine learning, the underlying methods and CPU hardware for processing vector data is now used to process other kinds of data.
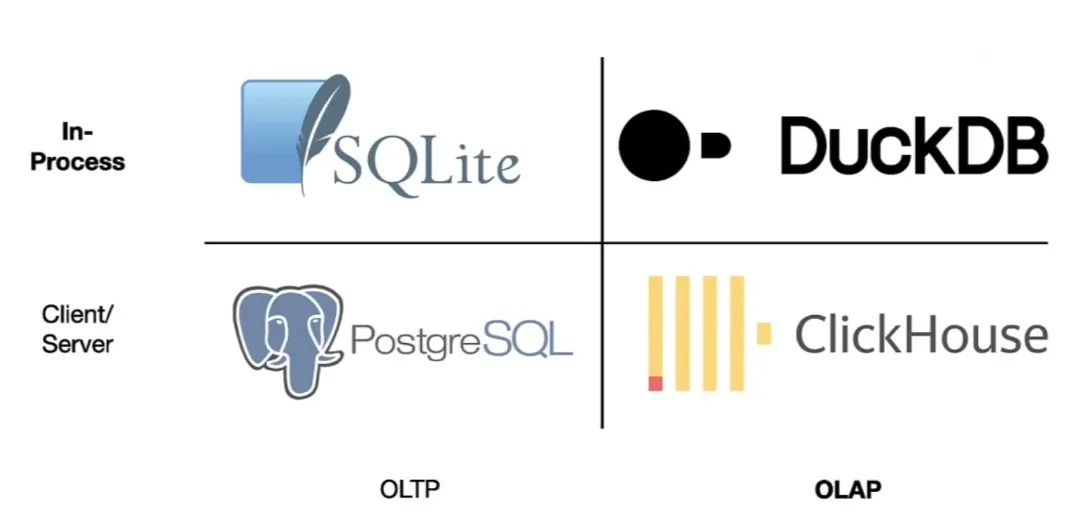
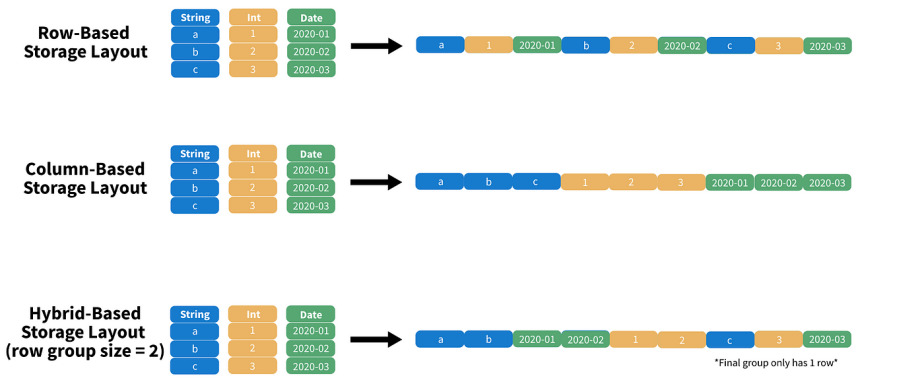
There are several databases on the market now like DuckDB, Big Query, Snowflake, and Crunchy Data Warehouse that make use of vectorized query execution to speed up analytics queries. Vectorized database queries split up and streamline queries into similar results over chunks of data of the same type. In a way, they’re treating columns of data like mathematical vectors. This can be much more powerful than reading data row by row. The power here also comes from the parallelization and effective CPU and IO usage.

The values processed with vectorized execution are typically treated as vectors in the sense that they’re contiguous batches of data elements. Surprisingly, they do not need to represent mathematical vectors—they can be any kind of data that fits the processing model.
Vectors are everywhere and they can mean virtually anything in a computerized context - especially now with AI - everything is or can be a vector.
Vectors and their uses are one of the main characters in the story of modern computing. An evolution from pen and ink math to modern ML algorithms. The beauty of the vector in its infinite use of numeric representation. From simple concepts like a point on the globe to computerized graphics and animation, and AI embeddings for any text or image.
Attributions
Hamilton’s Lecture on Vectors